 Ik hoor wel eens zeggen dat de raadsels op intussen… BLOG te moeilijk zijn. Bij een raadsel zweeft er een zekere waas in het oogvocht van de trouwe bloglezer. Edoch, we geven niet op. Het brein aanscherpen is ons doel. Hier gaan we!
Ik hoor wel eens zeggen dat de raadsels op intussen… BLOG te moeilijk zijn. Bij een raadsel zweeft er een zekere waas in het oogvocht van de trouwe bloglezer. Edoch, we geven niet op. Het brein aanscherpen is ons doel. Hier gaan we!
Een leraar staat voor een klas van 23 leerlingen. Hoe groot is de kans dat twee leerlingen dezelfde jaardag hebben? Eenvoudig, of toch niet?
Peter
PS: We gaan van een normaal jaar van 365 dagen uit.

Peter, ik twijfel er inmiddels niet aan dat je aanwezig en alert was tijdens alle lessen statistiek en kansrekening, duidelijk je stokpaardje. Daarom vraag ik je om een verklaring te geven waarom mijn vrouw en ik op de zelfde dag verjaren. Wat was is immers de kans dat een man en vrouw die op dezelfde dag verjaren in het huwelijksbootje stappen? Je mag uitgaan van een normaal jaar van 365 dagen.
Ha Thor, dat is wel heel eenvoudig. Die kans is 1/365. En omdat jullie blijkbaar een winnend duo zijn – wat is immers de kans van jullie treffen – nodig ik jullie uit deel uit te maken van onze beperkte Lottoclub: “De Poenpakkers”, waarbij elk lid indivueel op de hoogte gebracht wordt van effectieve winst via een mail met als aanspreektitel: “Hé chansard”. Geïnteresseerd? Mail me!
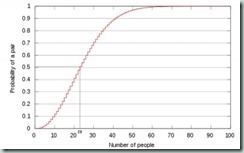
Eén kans op twee (volgens de grafiek..). De formule ken ik (begrijpelijkerwijze) niet meer
Ontwaar ik daar een doordachte acquisitie truc om een nieuw lid van de chansardclub te werven ? Geef toe, het raadsel was eigenlijk te simpel.
Correct Siegfried, en de vis heeft nog niet gebeten.
De berekening van het raadsel is als volgt.
Bereken eerst het tegendeel. Wat is de kans dat de eerste persoon niet op dezelfde dag verjaart als de tweede. Welnu, die kans is 364/365. Wat is de kans dat de derde persoon niet op dezelfde dag jarig is als de tweede en de eerste? Die kans is 363/365. En beide gecombineerd is dan 364/365*363/365. En doe dat dan nu voor 23 personen. Dus 364/365*363/365 * 362/365 …. 343/365=0.4927
En vermits “niet-op-dezelfde-dag-verjaren” en “op-dezelfde-dag-verjaren” onderling uitsluitende evenementen zijn, is de kans dat twee personen in de groep op dezelfde dag jarig zijn = 1-0.4927, en dus 0,5073